July 1, 2022
Welcome to the wonderful world of widgets. ¶
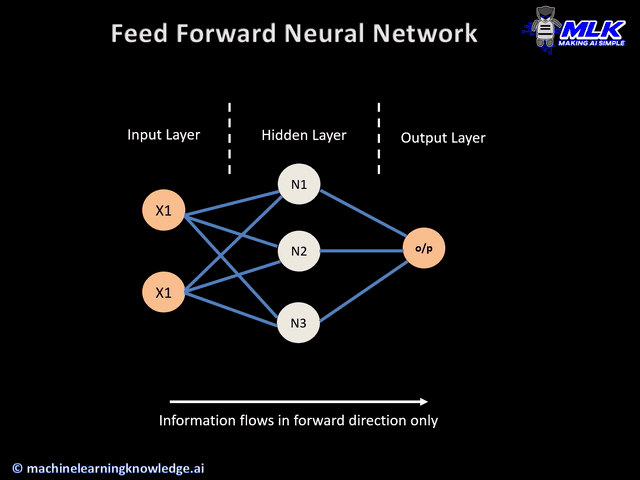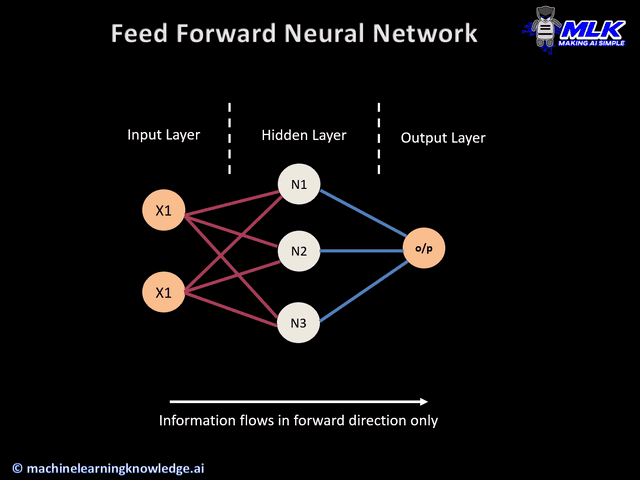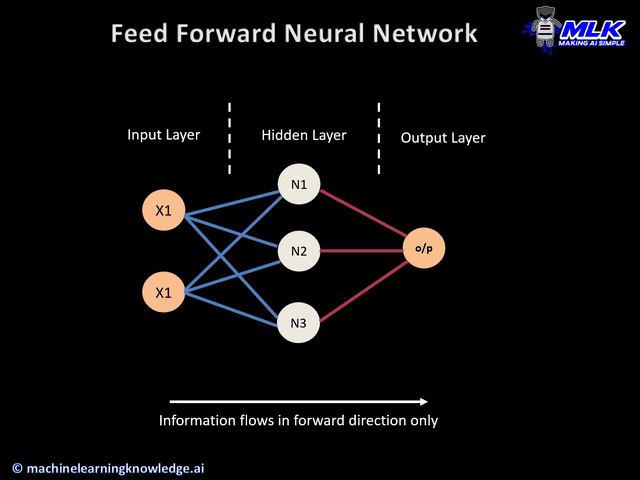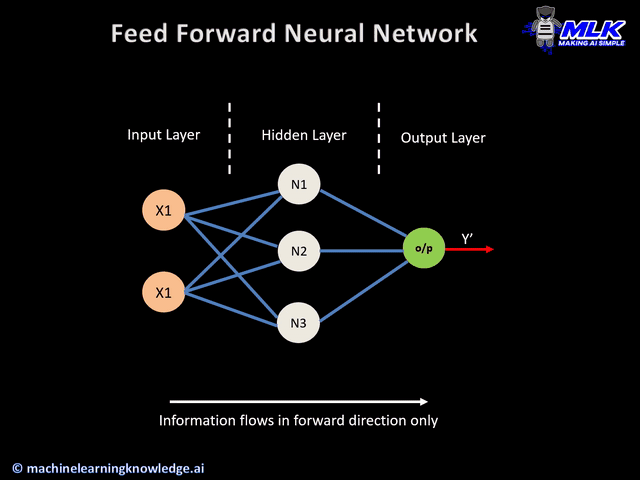
Today's widget is a predictive neural network.
STEPS
- Import Dependancies & Load Dataset
- Pre-process Data
a) check the dataset for unwanted columns, missing values, data type
b) separate target column from features columns - Split dataset into training and test data, then standarize data
- Build Neural Network
a) keras layers
b) complie by data type - Train Neural Network
- Visualize Performance and Probabilities
a) accuracy plot
b) loss plot
c) probability indices - Build Predictive System
Predictive System Output
1: benign
0: malignant
In [74]:
# https://www.youtube.com/watch?v=WGNI-k20GNo
#data array
import numpy as np
#data frame
import pandas as pd
#data collection, load breast cancer dataset from sklearn to pandas data frame
import sklearn.datasets
data = sklearn.datasets.load_breast_cancer()
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
Dataset Processing¶
In [75]:
print(data)
In [76]:
#load data into data frame
data_frame = pd.DataFrame(data.data, columns = data.feature_names)
#print last 5 rows
data_frame.tail()
Out[76]:
In [77]:
# adding target column to the data frame
data_frame["label"] = data.target
#print first 5 rows
data_frame.head()
Out[77]:
Check Data Structure and Modify as Needed¶
In [78]:
data_frame.info()
#tumple obj so don't need "()"; outputs (rows,columns)
data_frame.shape
#check for missing values
data_frame.isnull().sum()
data_frame.describe()
Out[78]:
In [79]:
#distribution of target variables (1: benign 357; 0: malignant 212)
data_frame["label"].value_counts()
Out[79]:
dataset has a slight imbalance; if difference greater, must employ up- or down-sampling for properly trained model¶
In [80]:
#mean for each column
data_frame.groupby("label").mean()
Out[80]:
In [81]:
#separate target column from the rest of the columns
# drop column: "axis = 1"
# drop row: "axis = 0"
x = data_frame.drop(columns="label", axis=1)
y = data_frame["label"]
In [82]:
# split data: 80% for training, 20% for testing
# shape (rows, columns) of original, training, and testing datasets
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y, random_state=2)
print(x.shape, x_train.shape, x_test.shape)
Split Then Standardize Processed Data¶
In [83]:
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y, random_state=2)
print(x.shape, x_train.shape, x_test.shape)
In [84]:
#standarize the data; fit data to training standard
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x_train_std = scaler.fit_transform(x_train)
x_test_std = scaler.transform(x_test)
Build Neural Network¶
In [85]:
#set seed to maintain network precision
from tensorflow import keras
import tensorflow as tf
tf.random.set_seed(3)
In [86]:
#layers setup
model = keras.Sequential([
keras.layers.Flatten(input_shape=(30,)), # input layer; 30 is the total columns - target column = features column
keras.layers.Dense(20, activation="relu"), # inter/hidden layer; 20 neurons
#keras.layers.Dense(23, activation="sigmoid), # another hidden layer; 30 neurons
keras.layers.Dense(2, activation="sigmoid") # output layer; number of classes: bengin and malignant
])
In [87]:
# compile network
model.compile(optimizer="adam",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"]
)
Train Neural Network¶
In [88]:
#run multiple times to improve accuracy to a certain limit
#ideal: small loss value, large accuracy value
history = model.fit(x_train_std, y_train, validation_split=0.1,epochs=10)
Visualize Neural Network Performance and Probabilities¶
In [89]:
import matplotlib.pyplot as plt
#Plot accuracy
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
plt.title("Neural Network Model Accuracy")
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.legend(["training data", "validation data"], loc="lower right")
Out[89]:
In [104]:
#Plot loss
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_loss"])
plt.title("Neural Network Model Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend(["training data", "validation data"], loc="center right")
Out[104]:
In [92]:
# Accuracy of Model on Test Data
# network will compare its prediction of the x_test_std data with the y_test data
loss, accuracy = model.evaluate(x_test_std, y_test)
print(accuracy)
In [93]:
print(x_test_std.shape) #original data shape
print(x_test_std[0]) #standardized data; [0] starts from first value
In [95]:
# model.predict() gives the probabilty the data point in x_test_std dataset is "1" vs "0"
y_predict = model.predict(x_test_std)
print(y_predict.shape)
print(y_predict[0])
#probabilty data is ("1: benign", "0: malignant")
In [96]:
# convert predication probability to class labels
# argmax function looks at the probabilities in the y_predict dataset and gives the index of the max value: "0" for the first value, "1" for the second value
# recall: [benign prob, malignant prob) in y_predict dataset
y_predict_labels = [np.argmax(i) for i in y_predict]
print(y_predict_labels)
Build Predictive System¶
In [105]:
# known benign data
input_data = (13.54,14.36,87.46,566.3,0.09779,0.08129,0.06664,0.04781,0.1885,0.05766,0.2699,0.7886,2.058,23.56,0.008462,0.0146,0.02387,0.01315,0.0198,0.0023,15.11,19.26,99.7,711.2,0.144,0.1773,0.239,0.1288,0.2977,0.07259)
# known malignant data
#input_data = (17.99,10.38,122.8,1001,0.1184,0.2776,0.3001,0.1471,0.2419,0.07871,1.095,0.9053,8.589,153.4,0.006399,0.04904,0.05373,0.01587,0.03003,0.006193,25.38,17.33,184.6,2019,0.1622,0.6656,0.7119,0.2654,0.4601,0.1189)
# change the input_data to a numpy array
input_data_as_numpy_array = np.asarray(input_data)
# reshape the numpy array as we are predicting for one data point
input_data_reshaped = input_data_as_numpy_array.reshape(1,-1)
# standarize input data; transform to fit with training data
input_data_std = scaler.transform(input_data_reshaped)
predict = model.predict(input_data_std)
predict_label = [np.argmax(predict)]
print(predict_label)
if (predict_label[0] == 0):
print("Malignant")
else:
print("Benign")